どうもこんにちは、カガクラムです。
今回は、
高校の物理でもたまに見かける、
「箱の中の理想気体の運動」の問題について、
解説していきたいと思います。
高校の物理や化学、難しいと感じる人も多いと思います。
実際に私も物理は大のニガテでした。

しかし、1問1問解き方をマスターしていけば、必ず成績も上がります。頑張っていきましょう!
問題:一辺の長さがℓ〔m〕の立方体の容器内に、一原子あたりの質量がm〔kg〕の単原子理想気体がN個ある。 内部エネルギーが3/2nRTであることを示せ。 ※ただし、気体定数をR〔J/(mol*K)〕とする。
今回↑の問題を取り扱っていきます。
一見難しい問題ですが、解き方はほとんど決まっています。
実は、基本的な公式から導き出せるので、さっそく見ていきましょう!
———————解答———————-
ある一つの単原子分子のx成分の速度を、Vx 〔m/s〕とする。
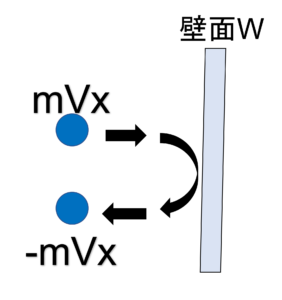
単原子分子1分子が、立方体のある壁面W(x軸に垂直な面)にぶつかるときの力積変化は、-mVx -(mVx)=-2mVx である。
ある単原子分子1分子が壁面Wに衝突してから、もう一度、壁面Wに衝突するまでには、2ℓ/Vx 〔s〕かかる。(一回衝突するのに2ℓ/Vx秒かかる)
よって逆数をとると、1秒あたりにVx/2ℓ〔/s〕回衝突する。
1秒あたりにVx/2ℓ回衝突し、一回の衝突で2mVx の力積が変化するので、1秒で
Vx/2ℓ × 2mVx = mVx²/ℓの力積が変化する。(→力・N)
容器の中にはN個の単原子分子が存在し、
N個のVx²の平均値を
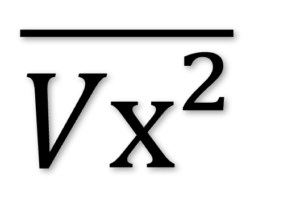 とすると、
とすると、
VxとVyとVzはそれぞれ等価なので、
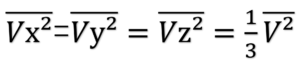
となる。
よって、容器内のN個の気体分子が及ぼす力Fは、
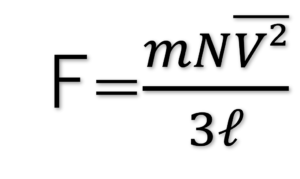 となる。
となる。
P=F/ℓ² なので、
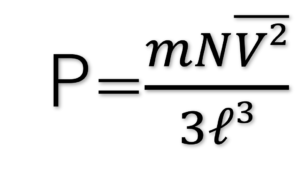 とおくことができる。
とおくことができる。
この式を変形すると、
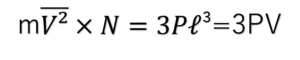 (Vは立方体の体積)
(Vは立方体の体積)
理想気体の内部エネルギーは、N個の単原子理想気体の運動エネルギーの総和と考えることができるため、両辺を2で割ると、
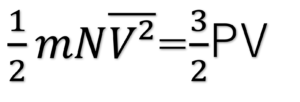
理想気体の状態方程式 PV=nRTより、
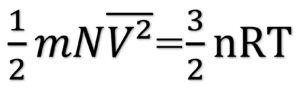
となる。 よって題意は示された。
解説
このような問題では、1つの分子がある壁面と衝突したときの力積変化から求めていきます。
理想気体と壁面は弾性衝突(e=1)すると考えるため、理想気体分子の速さは衝突前後で変わりません。(向きは変化します)
これで一回の衝突での力積変化が求まりました。
力積の単位とは、〔N・s〕なので、
1秒あたりの力積変化は力〔N〕となります。
よって、次は1秒で何回衝突するのかが知りたい。
理想気体は一辺がℓの立方体内を動き回っており、ある壁面Wに衝突してからもう一度衝突するまでの移動距離は2ℓ、速さはVxなので、もう一度衝突するまで2ℓ/Vx秒かかります。
これは、「一回衝突するのに〇秒かかる」ことを表しており、
逆数をとると「1秒あたりに〇回衝突する」ことを意味します。
「一回衝突するときの力積変化」は求まっているので、
力〔N〕も求まります。
力を面積ℓ²で割ると圧力になるため、圧力も求まります。
理想気体の内部エネルギーは各分子の運動エネルギーの総和と考えることが出来るので、「1/2mNV²=」の形にすると、
右辺が3/2nRTとなり、証明が完了します。


コメント